Homework #07
DUE: Monday, November 21, 2016 before class in Box B in the MAE department.
Problem 1¶
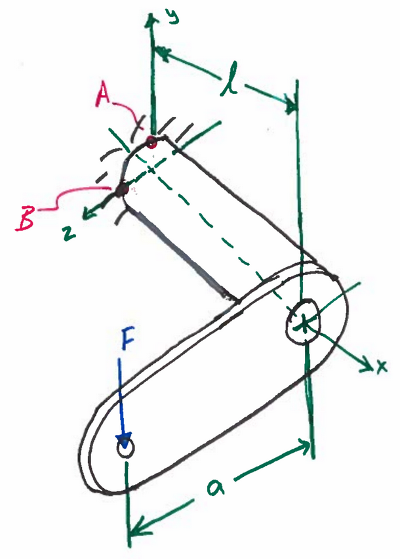
Determine the safety factors at points A and B for the bracket shown below. It is made of ASTM Class 50 Cast Iron (Table A-24). The variables have the following values: l = 6in, a = 8 in, d = 1.5 in, F = 1000 lb. Use the modified Mohr Theory.
Problem 2¶
(1) Estimate the endurance limit and the low cycle fatigue strength for an axially loaded ground steel specimen with \(S_{ut} = 150 \mathrm{ksi}\), \(d= 1.0 \mathrm{in}\), and \(T = 70^\circ \mathrm{F}\). (2) Determine the expected life for \(\sigma_a = 75 \mathrm{ksi}\) and \(\sigma_m=0 \mathrm{ksi}\).
Problem 3¶
Determine the required diameter for a round steel element that is axially loaded from -2500 to 2500 lb in fully reversed cycles. Assume it is ground, \(S_{ut} = 150 \mathrm{ksi}\), and is loaded at \(T = 70^\circ \mathrm{F}\). Determine the diameter for infinite life and \(10^3\) cycles.
Problem 4¶
Given a 2024-T3 aluminum specimen forged to \(2.0 \mathrm{in}\) round, determine the fatigue strength for \(3 \times 10^7\) cycles of loading for fully reversed torsion. Note that for non-ferrous metals, the unmodified fatigue strength is taken at \(N = 5 \times 10^8\) cycles (see Table A-24).
Problem 5¶
A simple hot rolled 1020 steel cantilever beam of length 0.6 m is loaded transversely at the end with a fully reversing load of \(\pm 5 \mathrm{kN}\). The beam has a rectangular cross section with a width of \(40 \mathrm{mm}\). What is the required height of the beam's cross section to guarantee safe operation up to \(N = 10^4 \mathrm{cycles}\) with a design factor of 2? Neglect any stress concentrations.