Problem 1

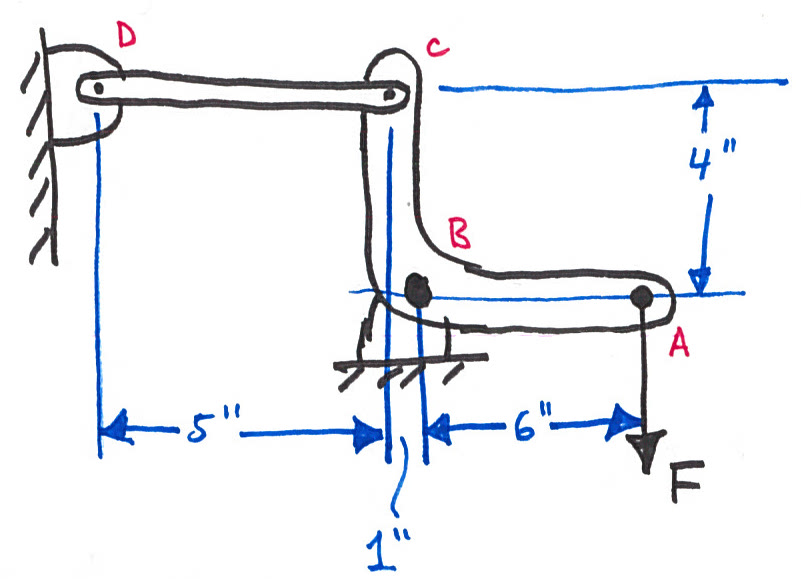
What is the maximum force \(F\) that can be applied to this system to ensure that the stress in member \(CD\) never exceeds 20 kpsi and the point \(A\) moves no more than 0.05"? Assume that the curved bar, \(ABC\), is much more rigid than \(CD\), i.e. assume it doesn't deform. The modulus of elasticity of the bar \(CD\) is \(6\times10^6 \frac{\mathrm{lb}}{\mathrm{in}^2}\) and the cross sectional area is \(0.25\mathrm{in}^2\). All of the joints are pin joints.

Problem 2

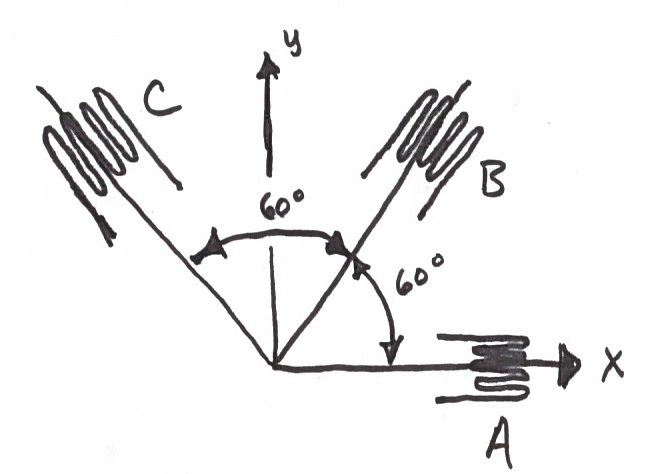
Three strain gauges are arranged in the orientation shown below on a free surface of a stressed member. The measured strains from the strain gauges are:

• \(\epsilon_A = 50\times10^{-6}\)
• \(\epsilon_B = 120\times10^{-6}\)
• \(\epsilon_C = 264\times10^{-6}\)

1. Derive the symbolic expressions for \(\epsilon_x, \epsilon_y, \epsilon_z\) for this configuration. Use only rational numbers, i.e. no decimal numbers and compute the state of strain.
2. Find the principal strains and directions.
3. If \(E=106\mathrm{GPa}\) and \(G=40\mathrm{GPa}\), what are the principal stresses and directions? Keep in mind that the normal stress on the surface is 0 because it is a free surface.
4. What is the maximum principal shear stress?

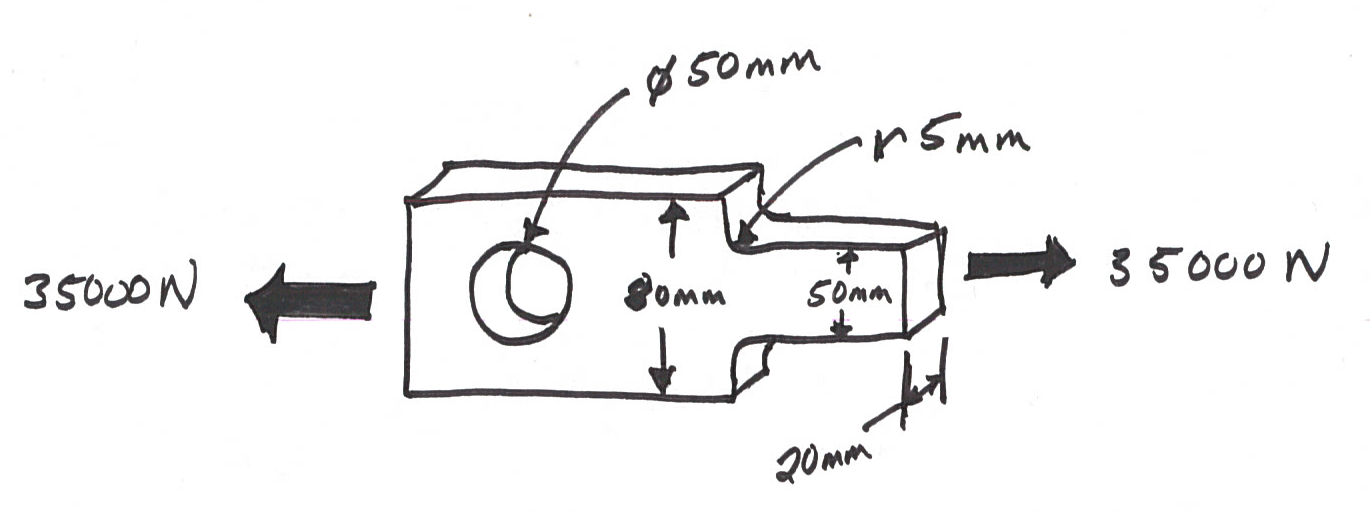
Problem 3

Find the maximum stress in the axially loaded member shown below. The hole is far enough away from the step down that the stress concentrations do not interact.

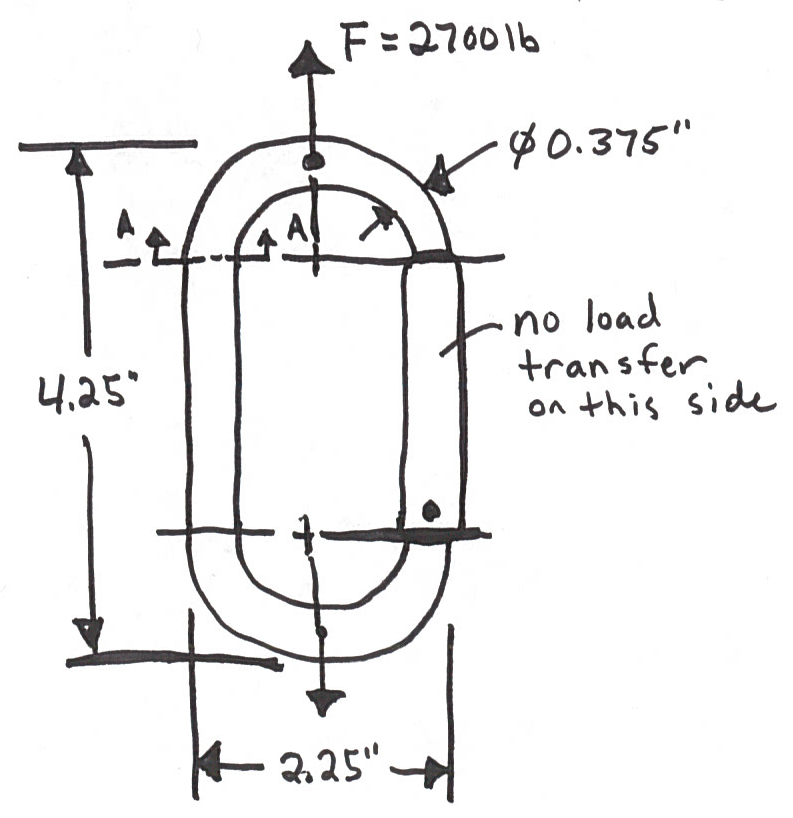
Problem 4

A rock climbing carabiner is shown below. The carabiner must be able to withstand a force up to 2700 lb to be safe enough to catch a 10 ft fall. What are the curved beam theory predicted stresses at the inner and outer points on section A-A? The cross section is circular.