Holonomic Constraints

Note

You can download this example as a Python script: configuration.py or Jupyter Notebook: configuration.ipynb.

import sympy as sm
import sympy.physics.mechanics as me
me.init_vprinting(use_latex='mathjax')

class ReferenceFrame(me.ReferenceFrame):

    def __init__(self, *args, **kwargs):

        kwargs.pop('latexs', None)

        lab = args[0].lower()
        tex = r'\hat{{{}}}_{}'

        super(ReferenceFrame, self).__init__(*args,
                                             latexs=(tex.format(lab, 'x'),
                                                     tex.format(lab, 'y'),
                                                     tex.format(lab, 'z')),
                                             **kwargs)
me.ReferenceFrame = ReferenceFrame

Learning Objectives

After completing this chapter readers will be able to:

• derive and specify the configuration constraint (holonomic constraint) equations for a system of connected rigid bodies

• numerically solve a set of holonomic constraints for the dependent coordinates

• apply point configuration constraints as a general approach to constraining a system

• calculate the number of generalized coordinates

• choose generalized coordinates

• calculate velocities when holonomic constraints are present

Four-Bar Linkage

Consider the linkage shown below:

Fig. 22 a) Shows four links in a plane \(A\), \(B\), \(C\), and \(N\) with respective lengths \(l_a,l_b,l_c,l_n\) connected in a closed loop at points \(P_1,P_2,P_3,P_4\). b) Shows the same linkage that has been separated at point \(P_4\) to make it an open chain of links.

This is a planar four-bar linkage with reference frames \(N,A,B,C\) attached to each bar. Four bar linkages are used in a wide variety of mechanisms. One you may be familiar with is this rear suspension on a mountain bicycle:

Fig. 23 Four bar linkage shown in blue, red, orange, and green used in the rear suspension mechanism of a mountain bicycle.

Cartemere, CC BY-SA 3.0 https://creativecommons.org/licenses/by-sa/3.0, via Wikimedia Commons

Depending on the length of the links, different motion types are possible. Fig. 24 shows some of the possible motions.

Fig. 24 Pasimi, CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, via Wikimedia Commons

A four bar linkage is an example of a closed kinematic loop. We can define this loop by disconnecting the loop at some location, \(P_4\) in our case, and forming the open loop vector equations to points that should coincide. In the case of Fig. 22 there are two vector paths to point \(P_4\) from \(P_1\), for example:

(85)\[\begin{split}\bar{r}^{P_4/P_1} & = l_n \hat{n}_x \\ \bar{r}^{P_4/P_1} & = \bar{r}^{P_2/P_1} + \bar{r}^{P_3/P_2} + \bar{r}^{P_4/P_3} = l_a\hat{a}_x + l_b\hat{b}_x + l_c\hat{c}_x\end{split}\]

For the loop to close, the two vector paths must equate. Keep in mind that we assume that the lengths are constant and the angles change with time. To define this loop in SymPy, setup the variables, reference frames, and points:

q1, q2, q3 = me.dynamicsymbols('q1, q2, q3')
la, lb, lc, ln = sm.symbols('l_a, l_b, l_c, l_n')

N = me.ReferenceFrame('N')
A = me.ReferenceFrame('A')
B = me.ReferenceFrame('B')
C = me.ReferenceFrame('C')

A.orient_axis(N, q1, N.z)
B.orient_axis(A, q2, A.z)
C.orient_axis(B, q3, B.z)

P1 = me.Point('P1')
P2 = me.Point('P2')
P3 = me.Point('P3')
P4 = me.Point('P4')

SymPy Mechanics will warn you if you try to establish a closed loop among a set of points and you should not do that because functions that use points have no way to know which vector path you desire to use. Instead you will establish positions among points on one open leg of the chain:

P2.set_pos(P1, la*A.x)
P3.set_pos(P2, lb*B.x)
P4.set_pos(P3, lc*C.x)

P4.pos_from(P1)

\[\displaystyle l_{c}\hat{c}_x + l_{b}\hat{b}_x + l_{a}\hat{a}_x\]

Now, create a vector for the other path to \(P_4\) outside of the Point position relationships:

r_P1_P4 = ln*N.x

With both vector paths written, we can form the left hand side of the following equation:

(86)\[\left( \bar{r}^{P_2/P_1} + \bar{r}^{P_3/P_2} + \bar{r}^{P_4/P_3} \right) - \bar{r}^{P_4/P_1} = 0\]

Use pos_from() for the open loop leg made of points and the additional vector:

loop = P4.pos_from(P1) - r_P1_P4
loop

\[\displaystyle l_{c}\hat{c}_x + l_{b}\hat{b}_x + l_{a}\hat{a}_x - l_{n}\hat{n}_x\]

This “loop” vector expression must equate to zero for our linkage to always be a closed loop. We have a planar mechanism, so we can extract two scalar equations associated with a pair of unit vectors in the plane of the mechanism. We can pick any two non-parallel unit vectors to express the components in, with the intuitive choice being \(\hat{n}_x\) and \(\hat{n}_y\).

fhx = sm.trigsimp(loop.dot(N.x))
fhx

\[\displaystyle l_{a} \cos{\left(q_{1} \right)} + l_{b} \cos{\left(q_{1} + q_{2} \right)} + l_{c} \cos{\left(q_{1} + q_{2} + q_{3} \right)} - l_{n}\]

fhy = sm.trigsimp(loop.dot(N.y))
fhy

\[\displaystyle l_{a} \sin{\left(q_{1} \right)} + l_{b} \sin{\left(q_{1} + q_{2} \right)} + l_{c} \sin{\left(q_{1} + q_{2} + q_{3} \right)}\]

For the loop to close, these two expressions must equal zero for all values \(q_1,q_2,q_3\). These are two nonlinear equations in three time varying variables called coordinates. The solution can be found if we solve for two of the time varying variables. For example, \(q_2\) and \(q_3\) can be solved for in terms of \(q_1\). We would then say that \(q_2\) and \(q_3\) depend on \(q_1\). These two equations are called holonomic constraints, or configuration constraints, because they constrain the kinematic configuration to be a loop. Holonomic constraints take the form of a real valued vector function:

(87)\[\bar{f}_h(q_1, \ldots, q_N, t) = 0 \textrm{ where } \bar{f}_h \in \mathbb{R}^M\]

\(N\) is number of coordinates that you have used to describe the system and \(M\) is the number of scalar constraint equations.

Warning

Holonomic constraints are defined strictly as equations that are function of the \(N\) time varying coordinates. It is true that these equations are only valid for a limited set of ranges for the constants in the equations, i.e. the lengths of the bars, but the range and combination constraints on the constants are not what we are considering here. Secondly, Eq. (87) does not represent inequality constraints. A coordinate may be constrained to a specific range, e.g. \(-\pi<q_1<\pi\), but these are not holonomic constraints in the sense defined here. Inequality constraints are generally dealt with using collision models to capture the real dynamics of forcefully limiting motion. See Collision for more information.

The four-bar linkage constraints are functions of configuration variables: time varying angles and distances. In our case the constraint equations are:

(88)\[\bar{f}_h(q_1, q_2, q_3) = 0 \textrm{ where } \bar{f}_h \in \mathbb{R}^2\]

and \(N=3\) and \(M=2\).

In SymPy, we’ll typically form this column matrix as so:

fh = sm.Matrix([fhx, fhy])
fh

\[\begin{split}\displaystyle \left[\begin{matrix}l_{a} \cos{\left(q_{1} \right)} + l_{b} \cos{\left(q_{1} + q_{2} \right)} + l_{c} \cos{\left(q_{1} + q_{2} + q_{3} \right)} - l_{n}\\l_{a} \sin{\left(q_{1} \right)} + l_{b} \sin{\left(q_{1} + q_{2} \right)} + l_{c} \sin{\left(q_{1} + q_{2} + q_{3} \right)}\end{matrix}\right]\end{split}\]

Exercise

Watt’s Linkage is a four-bar linkage that can generate almost straight line motion of the center point of the middle coupler link. Write the holonomic constraints for the Watt’s Linkage. The coupler link has a length of \(2a\), the left and right links have length \(b\). Make the vertical distance between the fixed points of the left and right lengths \(2a\) and the horizontal distance \((2-1/20)b\). Use the same reference frame and angle definitions as the four-bar linkage above.

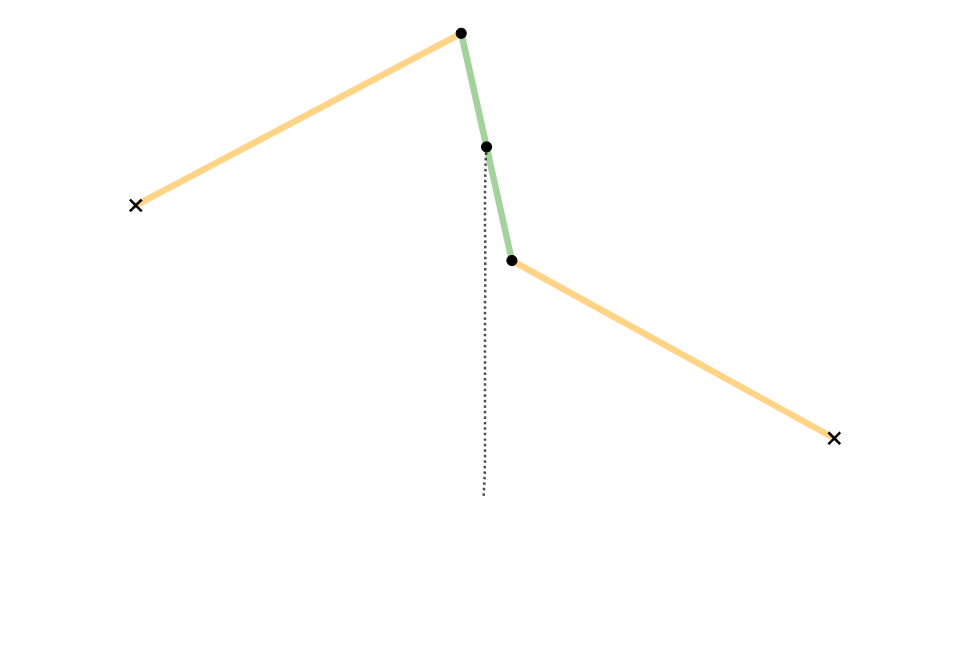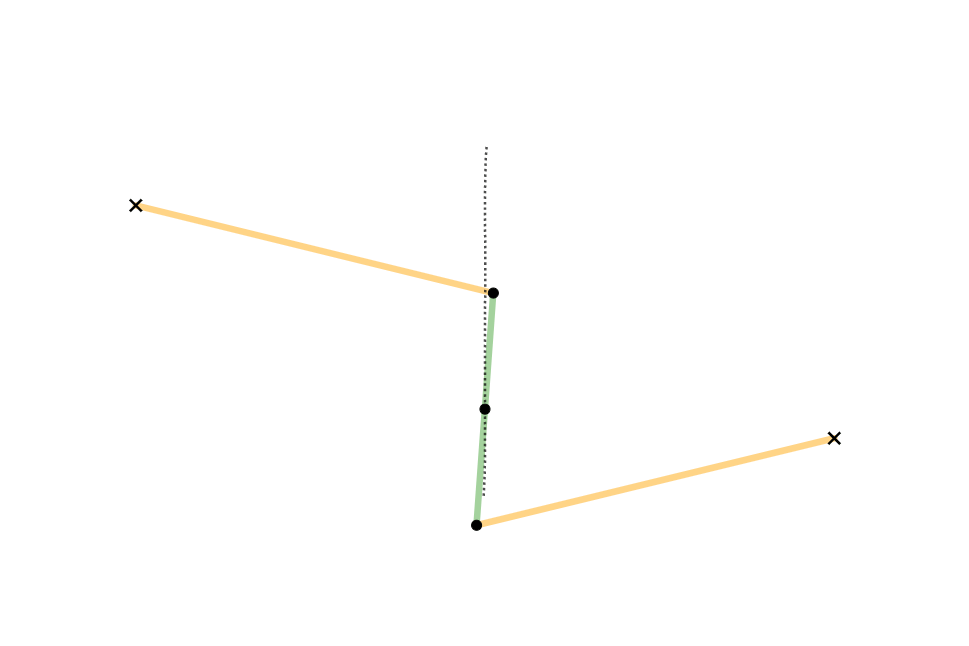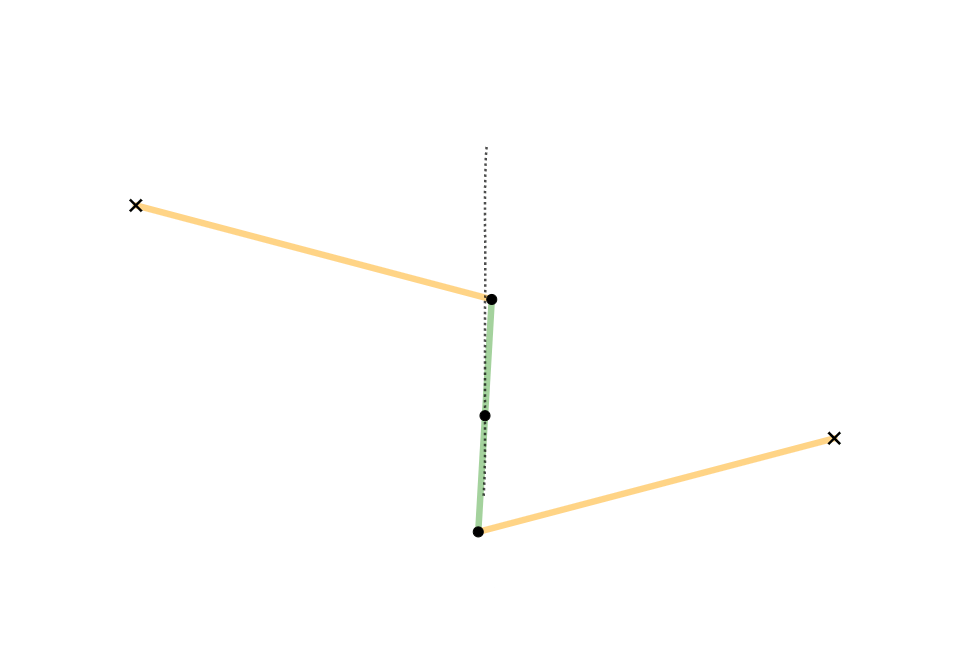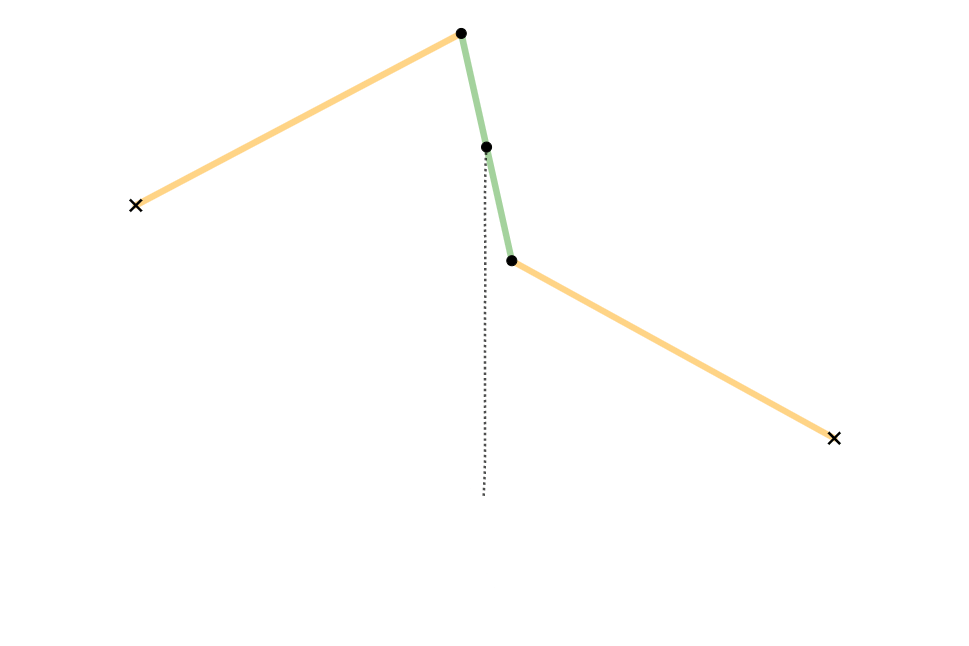
Fig. 25 Arglin Kampling, CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, via Wikimedia Commons

Solution

q1, q2, q3 = me.dynamicsymbols('q1, q2, q3')
a, b = sm.symbols('a, b')

N = me.ReferenceFrame('N')
A = me.ReferenceFrame('A')
B = me.ReferenceFrame('B')
C = me.ReferenceFrame('C')

A.orient_axis(N, q1, N.z)
B.orient_axis(A, q2, A.z)
C.orient_axis(B, q3, B.z)

P1 = me.Point('P1')
P2 = me.Point('P2')
P3 = me.Point('P3')
P4 = me.Point('P4')

P2.set_pos(P1, b*A.x)
P3.set_pos(P2, 2*a*B.x)
P4.set_pos(P3, b*C.x)

P4.pos_from(P1)

r_P1_P4 = (2 - sm.S(1)/20)*b*N.x - 2*a*N.y

loop = P4.pos_from(P1) - r_P1_P4

fh_watts = sm.trigsimp(sm.Matrix([loop.dot(N.x), loop.dot(N.y)]))
fh_watts

\[\begin{split}\displaystyle \left[\begin{matrix}2 a \cos{\left(q_{1} + q_{2} \right)} + b \cos{\left(q_{1} + q_{2} + q_{3} \right)} + b \cos{\left(q_{1} \right)} - \frac{39 b}{20}\\2 a \sin{\left(q_{1} + q_{2} \right)} + 2 a + b \sin{\left(q_{1} + q_{2} + q_{3} \right)} + b \sin{\left(q_{1} \right)}\end{matrix}\right]\end{split}\]

Solving Holonomic Constraints

Only the simplest of holonomic constraint equations may be solved symbolically due to their nonlinear nature, so you will in general need to solve them numerically. In Equations of Motion with Holonomic Constraints we will show how to solve them for simulation purposes, but for now SymPy’s nsolve() can be used to numerically solve the equations. If we choose \(q_2\) and \(q_3\) to be the dependent coordinates, we need to select numerical values for all other variables. Note that not all link length combinations result in a valid linkage geometry. Starting with the replacements,

import math  # provides pi as a float

repl = {
    la: 1.0,
    lb: 4.0,
    lc: 3.0,
    ln: 5.0,
    q1: 30.0/180.0*math.pi,  # 30 degrees in radians
}
repl

\[\displaystyle \left\{ l_{a} : 1.0, \ l_{b} : 4.0, \ l_{c} : 3.0, \ l_{n} : 5.0, \ q_{1} : 0.523598775598299\right\}\]

we can then formulate the constraint equations such that only \(q_2\) and \(q_3\) are variables:

fh.xreplace(repl)

\[\begin{split}\displaystyle \left[\begin{matrix}4.0 \cos{\left(q_{2} + 0.523598775598299 \right)} + 3.0 \cos{\left(q_{2} + q_{3} + 0.523598775598299 \right)} - 4.13397459621556\\4.0 \sin{\left(q_{2} + 0.523598775598299 \right)} + 3.0 \sin{\left(q_{2} + q_{3} + 0.523598775598299 \right)} + 0.5\end{matrix}\right]\end{split}\]

Generally, there may be multiple numerical solutions for the unknowns and the underlying algorithms require a guess to return a specific result. If we make an educated guess for the unknowns, then we can find the specific solution with nsolve():

q2_guess = -75.0/180.0*math.pi  # -75 degrees in radians
q3_guess = 100.0/180.0*math.pi  # 100 degrees in radians

sol = sm.nsolve(fh.xreplace(repl), (q2, q3), (q2_guess, q3_guess))
sol/math.pi*180.0  # to degrees

\[\begin{split}\displaystyle \left[\begin{matrix}-79.9561178980214\\108.613175851763\end{matrix}\right]\end{split}\]

Exercise

Find the angles of the remaining links in Watt’s Linkage if the middle linkage is rotated clockwise 5 degrees, \(a=1\), and \(b=4\).

Solution

The angle relative to vertical of the middle link is \(3\pi/2-(q_1+q_2)\), which we can use to solve for \(q_2\).

repl = {
    a: 1.0,
    b: 4.0,
    q2: 3.0*math.pi/2.0 - 5.0/180.0*math.pi - q1,
}
repl

\[\displaystyle \left\{ a : 1.0, \ b : 4.0, \ q_{2} : 4.62512251778497 - q_{1}\right\}\]

fh_watts.xreplace(repl)

\[\begin{split}\displaystyle \left[\begin{matrix}4.0 \cos{\left(q_{3} + 4.62512251778497 \right)} + 4.0 \cos{\left(q_{1} \right)} - 7.97431148549532\\4.0 \sin{\left(q_{3} + 4.62512251778497 \right)} + 4.0 \sin{\left(q_{1} \right)} + 0.00761060381650891\end{matrix}\right]\end{split}\]

q1_guess = 10.0/180.0*math.pi
q3_guess = 100.0/180.0*math.pi

sol = sm.nsolve(fh_watts.xreplace(repl), (q1, q3), (q1_guess, q3_guess))
sol/math.pi*180.0  # to degrees

\[\begin{split}\displaystyle \left[\begin{matrix}4.53780194767253\\90.3528330377729\end{matrix}\right]\end{split}\]

General Holonomic Constraints

If you consider a set of \(v\) points, \(P_1,P_2,\ldots,P_v\) that can move unconstrained in Euclidean 3D space, then one would need \(3v\) constraint equations to fix the points (fully constrain the motion) in that Euclidean space. For the four points in the four-bar linkage, we would then need \(3(4)=12\) constraints to lock all the points fully in place. The figure below will be used to illustrate the general idea of constraining the configuration of the four bar linkage.

Fig. 26 a) Four points in 3D space, b) four points constrained to 2D space, c) points are fixed to adjacent points by a fixed length, d) the first point is fixed at \(O\) in two dimensions, e) the fourth point is fixed in the \(y\) coordinate relative to \(O\).

Starting with a), there are the four points in 3D Euclidean space that are free to move. Moving to b), each of the four points can be then constrained to be in a plane with:

(89)\[\begin{split}\bar{r}^{P_1/O}\cdot\hat{n}_z = 0 \\ \bar{r}^{P_2/O}\cdot\hat{n}_z = 0 \\ \bar{r}^{P_3/O}\cdot\hat{n}_z = 0 \\ \bar{r}^{P_4/O}\cdot\hat{n}_z = 0\end{split}\]

where \(O\) is a point fixed in \(N\). This applies four constraints leaving 8 coordinates for the planar location of the points. Now at c) we constrain the points with:

(90)\[\begin{split}|\bar{r}^{P_2/P_1}| = l_a \\ |\bar{r}^{P_3/P_2}| = l_b \\ |\bar{r}^{P_4/P_3}| = l_c \\ |\bar{r}^{P_4/P_1}| = l_n\end{split}\]

These four constraint equations keep the points within the specified distances from each other leaving 4 coordinates free. In d) point \(P_1\) is fixed relative to \(O\) with 2 scalar constraints:

(91)\[\begin{split}\bar{r}^{P_1/O}\cdot\hat{n}_x = 0 \\ \bar{r}^{P_1/O}\cdot\hat{n}_y = 0\end{split}\]

Finally in e), \(P_4\) is constrained with the single scalar:

(92)\[\bar{r}^{P_4/P_1} \cdot \hat{n}_y = 0\]

Notice that we did not need \(\bar{r}^{P_4/P_1} \cdot \hat{n}_x = 0\), because (90) ensures the \(x\) coordinate of \(P_4\) is in the correct location.

These 11 constraints leave a single free coordinate to describe the orientation of \(A\), \(B\), and \(C\) in \(N\). When we originally sketched Fig. 22 most of these constraints were implied, i.e. we drew a planar mechanism with points \(P_1\) and \(P_4\) fixed in \(N\), but formally there are 12 coordinates needed to locate the four points and 11 constraints that constrain them to have the configuration of a four-bar linkage.

A general holonomic constraint for a set of \(v\) points with Cartesian coordinates is then ([Kane1985] pg. 35):

(93)\[f_h(x_1, y_1, z_1, \ldots, x_v, y_v, z_v, t) = 0\]

We include \(t\) as it is possible that the constraint is an explicit function of time (instead of only implicit, as seen above in the four-bar linkage example).

Generalized Coordinates

If a set of \(v\) points are constrained with \(M\) holonomic constraints then only \(n\) of the Cartesian coordinates are independent of each other. The number of independent coordinates is then defined as ([Kane1985] pg. 37):

(94)\[n := 3v - M\]

These \(n\) independent Cartesian coordinates can also be expressed as \(n\) functions of time \(q_1(t),q_2(t),\ldots,q_n(t)\) in such a way that the constraint equations are always satisfied. These functions \(q_1(t),q_2(t),\ldots,q_n(t)\) are called generalized coordinates and it is possible to find \(n\) independent coordinates that minimize the number of explicit constraint equations needed to describe the system’s configuration at all times \(t\). These generalized coordinates are typically determined by inspection of the system and there is a bit of an art to choosing the best set. But you can always fall back to the formal process of constraining each relevant point. If you describe your system with \(N\leq3v\) coordinates then:

(95)\[n := N - M\]

Take this simple pendulum with points \(O\) and \(P\) as an example:

If the pendulum length \(l\) is constant and the orientation between \(A\) and \(N\) can change, then the location of \(P\) relative to \(O\) can be described with the Cartesian coordinates \(x\) and \(y\). It should be clear that \(x\) and \(y\) depend on each other for this system. The constraint relationship between those two coordinates is:

(96)\[x^2 + y^2 = l^2\]

This implies that only one coordinate is independent, i.e. \(n=1\). More formally, the two points give \(3v=3(2)=6\) and there are 2 constraints for the planar motion of each point, 2 constraints fixing \(O\) in \(N\), and 1 constraint fixing the distance from \(O\) to \(P\), making \(M=5\) and thus confirming our intuition \(n=6-5=1\).

But there may be functions of time that relieve us from having to consider Eq. (96). For example, these two coordinates can also be written as as functions of the angle \(q\):

(97)\[\begin{split}x = l\cos q \\ y = l\sin q\end{split}\]

and if we describe the configuration with only \(q\), the constraint is implicitly satisfied. \(q\) is then a generalized coordinate because it satisfies \(n=1\) and we do not have to explicitly define a constraint equation.

Now, let’s return to the four-bar linkage example in Fig. 22 and think about what the generalized coordinates of this system are. We know, at least intuitively, that \(n=1\) for the four bar linkage. The four-bar linkage in Fig. 22 is described in a way that assumes a number of constraints are fulfilled, such as Eqs. (89) and (91), so we do not have to formally consider them.

Exercise

Are \(q_1,q_2,q_3\) generalized coordinates of the four-bar linkage? If not, why?

Solution

Any one of the \(q_1,q_2,q_3\) can be a generalized coordinate, but only one. The other two are depdendent due to the two constraints. We started with three coordinates \(q_1,q_2,q_3\) describing the open chain \(P_1\) to \(P_2\) to \(P_3\) to \(P_4\). Then we have two scalar constraint equations, leaving \(n=1\). Thus we can choose \(q_1\), \(q_2\), or \(q_3\) to be the indepdendent generalized coordinate.

If we take the general approach, starting with four unconstrained points, we need 11 constraints to describe the system, but if we select generalized coordinates to describe the system we only need 2 constraint equations (Eq. (88))! This simplifies the mathematical problem description and, as we will later see, is essential for obtaining the simplest forms of the equations of motion of a multibody system.

Calculating Additional Kinematic Quantities

You will often need to calculate velocities and accelerations of points and reference frames of systems with holonomic constraints. Due to the differentiation chain rule, velocities will be linear in the time derivatives of the coordinates and accelerations will be linear in the double time derivatives of the coordinates. Our holonomic constraints dictate that there is no relative motion between points or reference frames, implying that the relevant positions, velocities, and accelerations will all equate to zero.

Start by setting up the points for the four-bar linkage again:

P1 = me.Point('P1')
P2 = me.Point('P2')
P3 = me.Point('P3')
P4 = me.Point('P4')
P2.set_pos(P1, la*A.x)
P3.set_pos(P2, lb*B.x)
P4.set_pos(P3, lc*C.x)

In the four-bar linkage, \({}^N\bar{v}^{P_4}\) must be zero. We can calculate the unconstrained velocity like so:

P1.set_vel(N, 0)
P4.vel(N)

\[\displaystyle l_{c} \left(\dot{q}_{1} + \dot{q}_{2} + \dot{q}_{3}\right)\hat{c}_y + l_{b} \left(\dot{q}_{1} + \dot{q}_{2}\right)\hat{b}_y + l_{a} \dot{q}_{1}\hat{a}_y\]

The scalar velocity constraints can be formed in a similar fashion as the configuration constraints:

(98)\[\begin{split}{}^N\bar{v}^{P_4}\cdot\hat{n}_x = 0 \\ {}^N\bar{v}^{P_4}\cdot\hat{n}_y = 0\end{split}\]

sm.trigsimp(P4.vel(N).dot(N.x))

\[\displaystyle - l_{a} \sin{\left(q_{1} \right)} \dot{q}_{1} - l_{b} \left(\dot{q}_{1} + \dot{q}_{2}\right) \sin{\left(q_{1} + q_{2} \right)} - l_{c} \left(\dot{q}_{1} + \dot{q}_{2} + \dot{q}_{3}\right) \sin{\left(q_{1} + q_{2} + q_{3} \right)}\]

sm.trigsimp(P4.vel(N).dot(N.y))

\[\displaystyle l_{a} \cos{\left(q_{1} \right)} \dot{q}_{1} + l_{b} \left(\dot{q}_{1} + \dot{q}_{2}\right) \cos{\left(q_{1} + q_{2} \right)} + l_{c} \left(\dot{q}_{1} + \dot{q}_{2} + \dot{q}_{3}\right) \cos{\left(q_{1} + q_{2} + q_{3} \right)}\]

Notice that this is identical to taking the time derivative of the constraint vector function \(\bar{f}_h\):

t = me.dynamicsymbols._t
fhd = fh.diff(t)
fhd

\[\begin{split}\displaystyle \left[\begin{matrix}- l_{a} \sin{\left(q_{1} \right)} \dot{q}_{1} - l_{b} \left(\dot{q}_{1} + \dot{q}_{2}\right) \sin{\left(q_{1} + q_{2} \right)} - l_{c} \left(\dot{q}_{1} + \dot{q}_{2} + \dot{q}_{3}\right) \sin{\left(q_{1} + q_{2} + q_{3} \right)}\\l_{a} \cos{\left(q_{1} \right)} \dot{q}_{1} + l_{b} \left(\dot{q}_{1} + \dot{q}_{2}\right) \cos{\left(q_{1} + q_{2} \right)} + l_{c} \left(\dot{q}_{1} + \dot{q}_{2} + \dot{q}_{3}\right) \cos{\left(q_{1} + q_{2} + q_{3} \right)}\end{matrix}\right]\end{split}\]

We can see that the expressions are linear in \(\dot{q}_1,\dot{q}_2\) and \(\dot{q}_3\). If we select \(\dot{q}_2\) and \(\dot{q}_3\) to be dependent, we can solve the linear system \(\mathbf{A}\bar{x}=\bar{b}\) for those variables using the technique shown in Solving Linear Systems. First we define a column vector holding the dependent variables:

x = sm.Matrix([q2.diff(t), q3.diff(t)])
x

\[\begin{split}\displaystyle \left[\begin{matrix}\dot{q}_{2}\\\dot{q}_{3}\end{matrix}\right]\end{split}\]

then extract the linear terms:

A = fhd.jacobian(x)
A

\[\begin{split}\displaystyle \left[\begin{matrix}- l_{b} \sin{\left(q_{1} + q_{2} \right)} - l_{c} \sin{\left(q_{1} + q_{2} + q_{3} \right)} & - l_{c} \sin{\left(q_{1} + q_{2} + q_{3} \right)}\\l_{b} \cos{\left(q_{1} + q_{2} \right)} + l_{c} \cos{\left(q_{1} + q_{2} + q_{3} \right)} & l_{c} \cos{\left(q_{1} + q_{2} + q_{3} \right)}\end{matrix}\right]\end{split}\]

find the terms not linear in the dependent variables:

b = -fhd.xreplace({q2.diff(t): 0, q3.diff(t): 0})
b

\[\begin{split}\displaystyle \left[\begin{matrix}l_{a} \sin{\left(q_{1} \right)} \dot{q}_{1} + l_{b} \sin{\left(q_{1} + q_{2} \right)} \dot{q}_{1} + l_{c} \sin{\left(q_{1} + q_{2} + q_{3} \right)} \dot{q}_{1}\\- l_{a} \cos{\left(q_{1} \right)} \dot{q}_{1} - l_{b} \cos{\left(q_{1} + q_{2} \right)} \dot{q}_{1} - l_{c} \cos{\left(q_{1} + q_{2} + q_{3} \right)} \dot{q}_{1}\end{matrix}\right]\end{split}\]

and finally solve for the dependent variables:

x_sol = sm.simplify(A.LUsolve(b))
x_sol

\[\begin{split}\displaystyle \left[\begin{matrix}- \frac{\left(\frac{l_{a} \sin{\left(q_{2} \right)}}{\tan{\left(q_{3} \right)}} + l_{a} \cos{\left(q_{2} \right)} + l_{b}\right) \dot{q}_{1}}{l_{b}}\\\frac{l_{a} \left(l_{b} \sin{\left(q_{2} \right)} + l_{c} \sin{\left(q_{2} + q_{3} \right)}\right) \dot{q}_{1}}{l_{b} l_{c} \sin{\left(q_{3} \right)}}\end{matrix}\right]\end{split}\]

Now we can write any velocity strictly in terms of the independent speed \(\dot{q}_1\) and all of the other coordinates. free_dynamicsymbols() shows us what coordinates and their time derivatives present an any vector:

P4.vel(N).free_dynamicsymbols(N)

\[\displaystyle \left\{q_{1}, q_{2}, q_{3}, \dot{q}_{1}, \dot{q}_{2}, \dot{q}_{3}\right\}\]

Using the results in x_sol above we can write the velocity in terms of only the independent \(\dot{q}_1\):

(99)\[{}^N\bar{v}^A = v_x(\dot{q}_1, q_1, q_2, q_3)\hat{n}_x + v_y(\dot{q}_1, q_1, q_2, q_3)\hat{n}_y + v_z(\dot{q}_1, q_1, q_2, q_3)\hat{n}_z\]

Making the substitutions gives the desired result:

qd_dep_repl = {
  q2.diff(t): x_sol[0, 0],
  q3.diff(t): x_sol[1, 0],
}
qd_dep_repl

\[\displaystyle \left\{ \dot{q}_{2} : - \frac{\left(\frac{l_{a} \sin{\left(q_{2} \right)}}{\tan{\left(q_{3} \right)}} + l_{a} \cos{\left(q_{2} \right)} + l_{b}\right) \dot{q}_{1}}{l_{b}}, \ \dot{q}_{3} : \frac{l_{a} \left(l_{b} \sin{\left(q_{2} \right)} + l_{c} \sin{\left(q_{2} + q_{3} \right)}\right) \dot{q}_{1}}{l_{b} l_{c} \sin{\left(q_{3} \right)}}\right\}\]

P4.vel(N).xreplace(qd_dep_repl)

\[\displaystyle l_{c} \left(\frac{l_{a} \left(l_{b} \sin{\left(q_{2} \right)} + l_{c} \sin{\left(q_{2} + q_{3} \right)}\right) \dot{q}_{1}}{l_{b} l_{c} \sin{\left(q_{3} \right)}} + \dot{q}_{1} - \frac{\left(\frac{l_{a} \sin{\left(q_{2} \right)}}{\tan{\left(q_{3} \right)}} + l_{a} \cos{\left(q_{2} \right)} + l_{b}\right) \dot{q}_{1}}{l_{b}}\right)\hat{c}_y + l_{b} \left(\dot{q}_{1} - \frac{\left(\frac{l_{a} \sin{\left(q_{2} \right)}}{\tan{\left(q_{3} \right)}} + l_{a} \cos{\left(q_{2} \right)} + l_{b}\right) \dot{q}_{1}}{l_{b}}\right)\hat{b}_y + l_{a} \dot{q}_{1}\hat{a}_y\]

P4.vel(N).xreplace(qd_dep_repl).free_dynamicsymbols(N)

\[\displaystyle \left\{q_{1}, q_{2}, q_{3}, \dot{q}_{1}\right\}\]

The holonomic constraints will have to be solved numerically as described in Solving Holonomic Constraints, but once done only the independent \(\dot{q}_1\) is needed.